R: Guten Morgen!
A: Guten Morgen!
R: Gibt es noch Kaffee?
A: Ja, ich schenke dir einen Kaffee ein, setz dich hin!
R: Danke für den Kaffee, er ist frisch!
A: Gern geschehen!
R: Wie sieht es mit dem Wetter aus?
A: Dem Wetterbericht zufolge regnet es heute den ganzen Tag durch, zeitweise stark und stürmisch. Draussen ist es windig, kalt und nass.
R: Zum Glück haben wir gestern die Wohnung aufgeräumt und eingekauft. Der Kaffee hat mir geschmeckt. Kann ich noch einen Kaffee haben?
A: Das freut mich zu hören. Ich mache noch Einen!
R: Ich schlage vor, wir bleiben heute zu Hause.
A: Dann setzen wir uns an den Küchentisch und diskutieren über Dieses und Jenes.
R: Ich bin einverstanden.
A: Der Kaffee ist bereit, ich schenke dir und mir einen frischen Kaffee ein und setzte mich zu dir an den Tisch.
R: Danke dir, der Kaffee riecht gut!
A: Erinnerst du dich an die Physikstunde und Archimedes?
R: Klar. Archimedes entdeckte, wenn ein Gegenstand in einen Eimer, der bis zum Rand mit Wasser gefüllt ist, hinein taucht, verrät die verdrängte Wassermenge das Volumen des Gegenstandes.
A: Bestimmt. Zu seiner Zeit war Archimedes eine berühmte Persönlichkeit. Eines Tages, so die Legende, stieg er ins Bad. Als er sich jedoch ins Wasser legte, wurde ihm schlagartig klar, dass sein Körper eine gewisse Menge an Wasser verdrängte, das über den Wannenrand trat. Daraus formte sich in seinem Kopf auf der Stelle eine Lösung. Von Freude überwältig, sprang Archimedes aus der Wanne und rannte Pudel nackt durch die Stadt, wobei er laut «Heureka!» («Ich habe es!) gerufen haben soll.
R: Archimedes waren zwei wichtige Dinge klar geworden: Zum einen, wenn ein Körper ins Wasser eintaucht, verdrängt er dabei auch Wasser, zum anderen, jeder Körper fühlt sich im Wasser leicht an, denn er erfährt einen Antrieb, der dem Gewicht des von ihm verdrängten Wassers entspricht. Dies hatte der Physiklehrer als archimedisches Prinzip benannt.
Bild. Eine Darstellung von Archimedes in der Badewanne
A: Archimedes sind viele andere friedliche Erfindungen zu verdanken, unter anderem eine hydraulische Schraube zur Wasserförderung und ein Planetarium, dass die Bewegung der Himmelskörper zeigte. Zu seinen vielen Leistungen gehörten unter anderem allgemein anwendbare Methoden zur Ermittlung der Fläche einer Vielfalt von Figuren in der Ebene und des Volumens von Körpern, die von allen möglichen Arten von gekrümmten Oberflächen umschlossen sind. In der Physik entdeckte er die Gesetzte, nach denen sich schwimmende Körper verhalten, und legte so den Grundstein für Hydrostatik. Ausserdem errechnete er die Hebelgesetzte. Er führte astronomische Beobachtungen zur Bestimmung der Jahreslänge und der Entfernung zu den Planeten durch. Archimedes hatte Achtung vor der heliozentrischen Theorie des Astronomen Aristarch von Samos (im weiteren Verlauf der Abhandlung korrigiert er eine von dessen Hypothesen). Im Universum des Aristrach drehten sich die Erde und die Planeten um eine stationäre Sonne im Zentrum des Systems. Denke nur daran, dieses Modell wurde 1800 Jahre vor Kopernikus ersonnen.
Bild. Archimedischen Körper
R: Ich wusste nicht, dass Archimedes so viel geleistet hatte, er war ein brillanter Wissenschaftler.
A: Und als Letztes schliesslich wird Archimedes’ Status als Magier manifestiert durch seine Vorwegnahme der Integral- und Differentialrechnung – eines Zweigs der Mathematik, dessen formale Entwicklung erst gegen Ende des 17. Jahrhunderts von dem Engländer Isaac Newton und unabhängig von diesem von dem Deutschen Gottfried Wilhelm Leibniz geleistet wurde. Man kann schon daraus schliessen, dass Archimedes die Welt der Mathematik und die Wahrnehmung ihrer Relation zum Kosmos in tiefgreifender Weise verändert hatte. Durch eine faszinierende Kombination von theoretischem und praktischem Interesse erbrachte er den ersten empirischen – nicht mythischen – Beweis für eine augenscheinliche mathematische Beschaffenheit der Natur. Die Vorstellung von der Mathematik als Sprache des Universums, und auch die Vorstellung eines von Mathematik betreibenden Gottes, wurzelt demnach in Archimedes’ Arbeit.
Bild. Grundlagen der Integralrechnung.
R: Ich habe Lust auf Kuchen. Ich habe gestern einen grossen Schokoladenkuchen gekauft und möchte jetzt ein Stück von ihm ausprobieren.
A: Lädst du mich zu Kaffee und Kuchen ein?
R: Ich hole den Kuchen aus dem Kühlschrank heraus, schneide ihn in Stücke, gebe dir und mir je ein Stück und bereite den Kaffee vor!
A: Ich danke dir. Der Kuchen ist schmackhaft, er gefällt mir!
R: Das freut mich zu hören. Ich schenke dir und mir noch einen frischen Kaffee ein und setze mich. Du hast recht, der Kuchen ist lecker.
A: Woran erinnerst du dich noch, wenn du an Physikstunden in der Schule denkst?
R: Viele dieser Stunden waren mit Mathematik, Mechanik, Gleichungen, Messungen und Formeln verbunden. Es waren auch viele Namen wie Pythagoras, Platon, Euklid, Aristoteles, und auch Johannes Kepler, René Descartes, Leibniz, Newton. Sie waren Wissenschaftler und auch Philosophen.
A: Nun, ich glaube, als Galileo Galilei, Rene Descartes und Isaac Newton ihre Ansichten äusserten, hat das moderne wissenschaftliche Zeitalter begonnen. Damals wurde die neue wissenschaftliche Auffassung ständig erweitert, als man in den irdischen und astronomischen Daten Muster entdeckte, die den Menschen immer deutlicher vor Augen führen, dass all dem Kommen und Gehen der Welt sowie des Kosmos eine Ordnung zugrunde liegt, die sich logischem Denken und mathematischer Analyse erschliesst. Diese Pioniere des modernen wissenschaftlichen Denkens vertraten die Auffassung, dass die Geschehnisse im Universum, richtig betrachtet, nicht nur erklärbar, sondern auch vorhersagbar sind. Damit war das Vermögen der Wissenschaft, Aspekte der Zukunft schlüssig und quantitativ vorherzusagen, zu Tage getreten. Erinnerst du dich an die Physikstunde, in der der Physiklehrer uns die Gravitationsgesetzte erklärt und sie darstellt?
R: Ich erinnere mich daran. Der Physiklehrer unterrichtete seit vielen Jahren. Er begann mit einem kurzen Gedicht:
«Natur und Naturgesetz lagen tief verborgen in der Nacht,
Da sprach Gott: Es wurde Newton! Und alles ward Licht.»
Danach erklärte er uns; Bei einem Spaziergang habe Newton einen Apfel fallen sehen. Durch dieses Ereignis nämlich der fallende Apfel wurde Newton klar, der Apfel, der Mond und die Planeten der gleichen Anziehungskraft und zwar dem gleichen Gravitationsgesetzt gehorchen, dass sie alle dem gleichen quadratischen Abstandgesetzt unterworfen sind. Newton beschreibt die Gesetzte der Mechanik, das heisst, die Bewegungsgesetzte, welche die Bahnen aller irdischen und himmlischen Körper bestimmen. Dann begann er die Formeln an die Tafel zu schreiben.
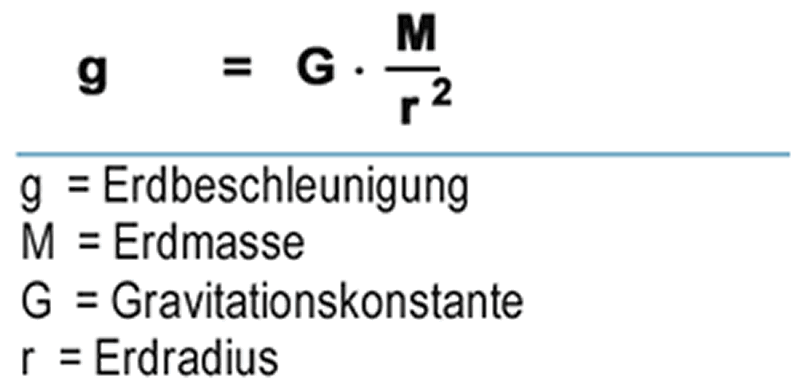
Bild. Eines von Newtons Formeln
A: Du erinnerst dich klar an diese Stunde!
R: Am Ende der Stunde fasste der Lehrer alles zusammen und deutete daraufhin, dass Newton uns die ewigen Bewegungsgesetzte schenkte. Mit Hilfe dieser Gesetzte haben die Menschen Maschinen entworfen, die Dampfkraft genutzt und Lokomotiven aufgebaut, die ihrerseits die Voraussetzung für die industrielle Revolution und die moderne Zivilisation schufen. Heute werden beim Bau jedes Wolkenkratzers, jeder Brücke und jeder Rakete Newtons Bewegungsgesetzte zugrunde gelegt.
Bild. Newton Navarro Bridge in Brasilien.
A: Newton beschäftigte sich mit fallenden Äpfeln (so heisst es zumindest) und der Umlaufbahn des Mondes. Mit einer Hand voll mathematischer Gleichungen fasste er alles zusammen, was über die Bewegungen auf der Erde und im Himmel bekannt war, und steckte damit die Grenzen dessen ab, was später als klassische Physik bezeichnet werden sollte. In den Jahrzehnten nach Newton wurden seine Gleichungen zu einem komplizierten mathematischen System ausgebaut, das ihren Geltungsbereich und praktischen Nutzen erheblich erweiterte. Selbst heute noch, mehr als dreihundert Jahre später, findet man Newtons Gleichungen weltweit an den Wandtafeln bei physikalischen Einführungskursen, auf den Flugplänen, mit denen die NASA die Bahnen von Raumfahrzeugen berechnet, und eingebettet in die komplizierten Berechnungen modernster Forschungsvorhaben. Newton fasste eine Vielzahl physikalischer Phänomene in einem einzigen theoretischen Rahmen zusammen und formulierte in seinem Werk Principia Mathematica mit ein paar kurzen Sätzen eine Vorstellung von Raum und Zeit, in der er diese zu absoluten und unwandelbaren Grössen erklärte und das Universum dergestalt mit einem unbeweglichen und unwandelbaren Schauplatz versah. Laut Newton bilden Raum und Zeit ein unsichtbares Gerüst, das dem Universum Gestalt und Struktur verleiht.
Bild. Die komplizierte, auf newtonschen Mechanik basierte Berechnungen bei den Raumsonden.
R: Wie definierst du die klassische Physik?
A: Der Begriff «Klassische Physik» bezieht sich auf die Physik vor der Quantenmechanik. Die klassische Physik umfasst Newtons Gleichungen für die Bewegung eines Teilchens, die Theorie von Maxwell über elektromagnetische Felder und Einsteins Allgemeine Relativitätstheorie. Aber sie ist mehr als nur bestimmte Theorien zu bestimmten Beobachtungen; sie ist eine Ansammlung von Prinzipien und Regel – eine zugrundeliegende Logik – die alle Phänomene beschreibt. In der klassischen Physik können wir, wenn wir die Bewegungen aller Teilchen im gegenwärtigen Augenblick kennen, die Zukunft vorhersagen. Die allgemeine Regel zur Darstellung der Bewegung aller Teilchen und Gegenstände wird klassische Mechanik genannt.
R: Wir haben schon mal über Elektromagnetismus diskutiert. Ich schlage vor; wir diskutieren jetzt über Relativität!
A: Nun, die Relativitätsrevolution dauerte von 1905 bis 1915; in diesem Zeitraum entwickelte Einstein seine spezielle und allgemeine Relativitätstheorie. Während er sich mit den Rätseln der Elektrizität, des Magnetismus und der Lichtbewegung auseinandersetzte, erkannte Einstein, dass Newtons Raum-Zeit- Konzept, der Hauptpfeiler der klassischen Physik, so nicht stimmen konnte. Er fand heraus, dass Raum und Zeit nicht unabhängig und absolut sind, wie Newton angenommen hatte, sondern miteinander verflochten und in einer Weise relativ, die aller alltäglichen Erfahrung spottet. Später revidierte Einstein die Gesetzte der Gravitationsphysik und er beweist nicht nur, dass Raum und Zeit Teile eines einheitlichen Ganzen sind, sondern zeigte auch, dass sie über ihre Verzerrung und Krümmung an der kosmischen Entwicklung mitwirken. Raum und Zeit erwiesen sich in Einsteins Entwurf als flexibel und dynamisch. Einstein entdeckte, dass die Krümmung der Raumzeit die Ursache ist, die die Gravitation erzeugt und somit, dass die Raumzeit wie ein Gewebe strukturiert ist und sich wellenförmig bewegt sowie ausbereitet. Einsteins Geleichung zeigt, dass die Materie konzentrierte Energie ist.
Bild. Einsteins berühmte Formel.
R: Möchtest du ein Glas Wasser?
A: Gerne!
R: Hier stelle ich dein Glas Wasser auf den Tisch!
A: Danke, das Wasser ist das beste Getränk, wenn ich Durst habe!
R: Momentan denke ich an die Zeit des Studiums!
A: Das ist lange her. Woran denkst du?
R: Ich erinnere mich gerade an jene Stunde, in der der Dozent uns mitteilte, dass die Gravitationstheorie, die wir gerade in der Schule gelernt hatten, falsch war.
A: Ich erinnere mich gut daran. Du warst so wütend und hattest den Dozenten sofort gefragt; Warum sollte man uns eine Theorie beibringen, von der man wusste, dass sie nicht korrekt war?
R: Ja, diese Erinnerung … !
A: Weisst du noch, welche Antwort hat dir der Dozent gegeben?
R: Ich erinnere mich nicht gut daran. Was hat er geantwortet?
A: Er fragte zuerst nach deinem Namen. Danach sagte er: Universitäten gehören zum Kulturministerium, die Schulen hingegen gehören zum Bildungs- und Erziehungsministerium. Bitte wenden Sie sich ans zuständige Ministerium, vielleicht bekommen Sie dort eine Antwort auf Ihre Frage!
R: Er hatte immer alle Fragen beantwortet!
A: Der Dozent hatte jedoch die Sache zu stark vereinfacht. Er bemerkte: Newtons Theorie war nicht falsch; sie war bloss eine Annährung, die unter den meisten Umständen unglaublich gut funktioniert. Für ein breites Spektrum von Parametern, wie Geschwindigkeit, Entfernung, Masse und so weiter sagt Newtons Physik die Gravitationskräfte ziemlich genau voraus. Newtons Gesetzt beschreibt die Bewegung eines Balls bewundernswert gut. Die präzisere, ihr zugrundeliegende Theorie ist aber die der Relativität, und nur mit der kommt man zu messbar unterschiedlichen Vorhersagen, wenn man es mit extrem hohen Geschwindigkeiten oder grossen Mengen von Masse oder Energie zu tun bekommt.
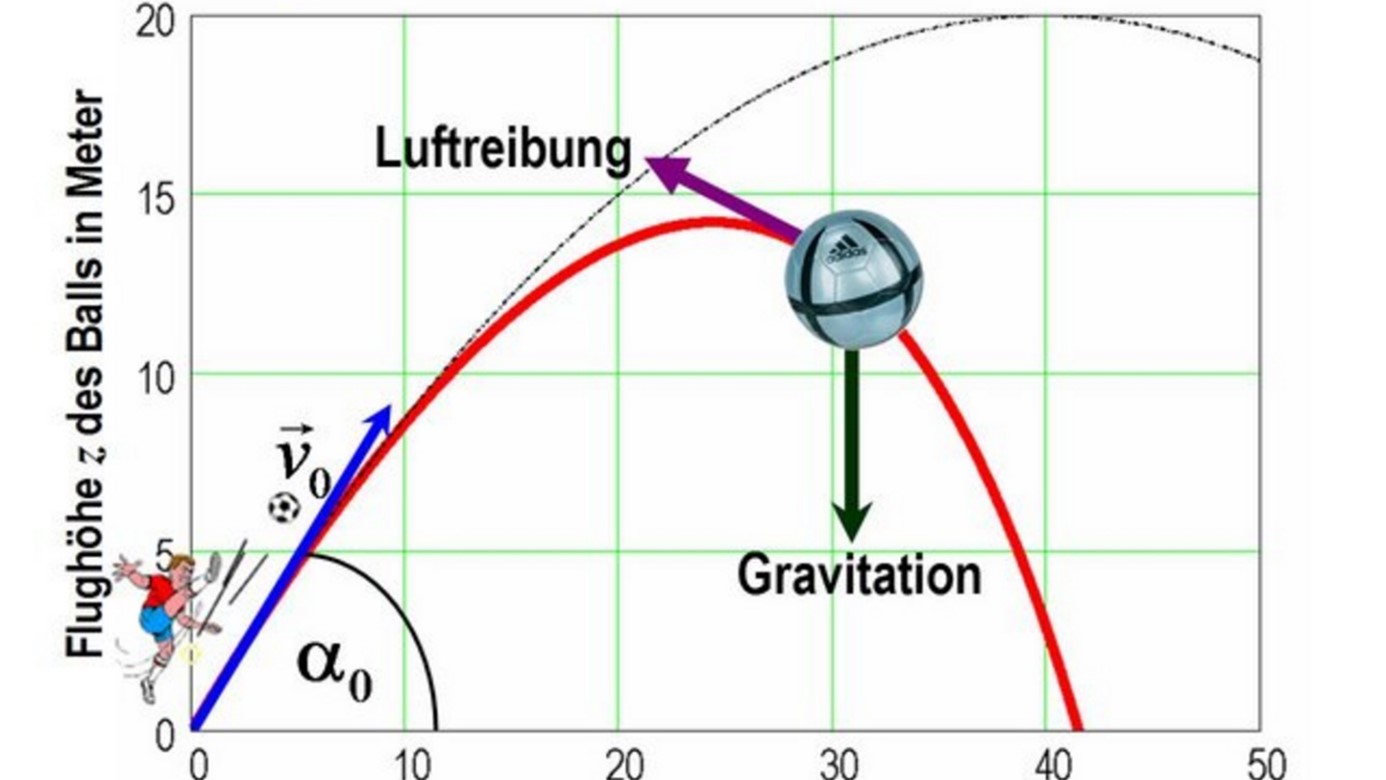
Bild. Die Flugbahn eines Balls.
R: Es wurde gesagt, dass eine Folge der speziellen Relativitätstheorie die Atombombe ist!
A: Nun, spezielle Relativitätstheorie ist eine Theorie aus dem Jahr 1905 und beruht auf der Konstanz der Lichtgeschwindigkeit. Zu ihren Konsequenzen gehören: die Zeit verlangsamt sich, die Masse nimmt zu und Entfernungen schrumpfen umso mehr, je rascher sie sich bewegen. Ferner ist die Beziehung zwischen Materie und Energie durch die Formel E (Energie) = m (Masse) c² (Lichtgeschwindigkeit, hoch zwei) gegeben. Zweifellos ist die Atombombe eine Folge der speziellen Relativitätstheorie. In einer Atombombe wird die Materie in die Energie umgewandelt.
Bild. Einsteins Relativitätsrevolution
R: Einstein gehört zu berühmten Wissenschaftlern unserer Zeit!
A: Auf jeden Fall. Einstein betrachtete Gravitation nicht länger als eine Kraft, die direkt auf ein Objekt wirkt. Vielmehr beschreibt er sie als eine Verzerrung der Raumzeitgeometrie, die die unterschiedlichen Beschleunigungen widerspiegelt, welche erforderlich sind, damit an unterschiedlichen Orten die Gravitation aufgehoben werden kann. Die Raumzeit ist nicht länger der belanglose Hintergrund eines Ereignisses – sie spielt aktiv mit. Mit Einsteins allgemeiner Relativitätstheorie lässt sich die Schwerkraft als Krümmung der Raumzeit begreifen, die wiederum von der vorhandenen Materie und Energie bestimmt wird. Die allgemeine Relativitätstheorie ist experimentell mit einer Genauigkeit von mehr als 99,7 Prozent bestätigt worden und sagt die Existenz von Schwarzen Löchern und die Expansion des Universums sowie Gravitationswellen voraus.
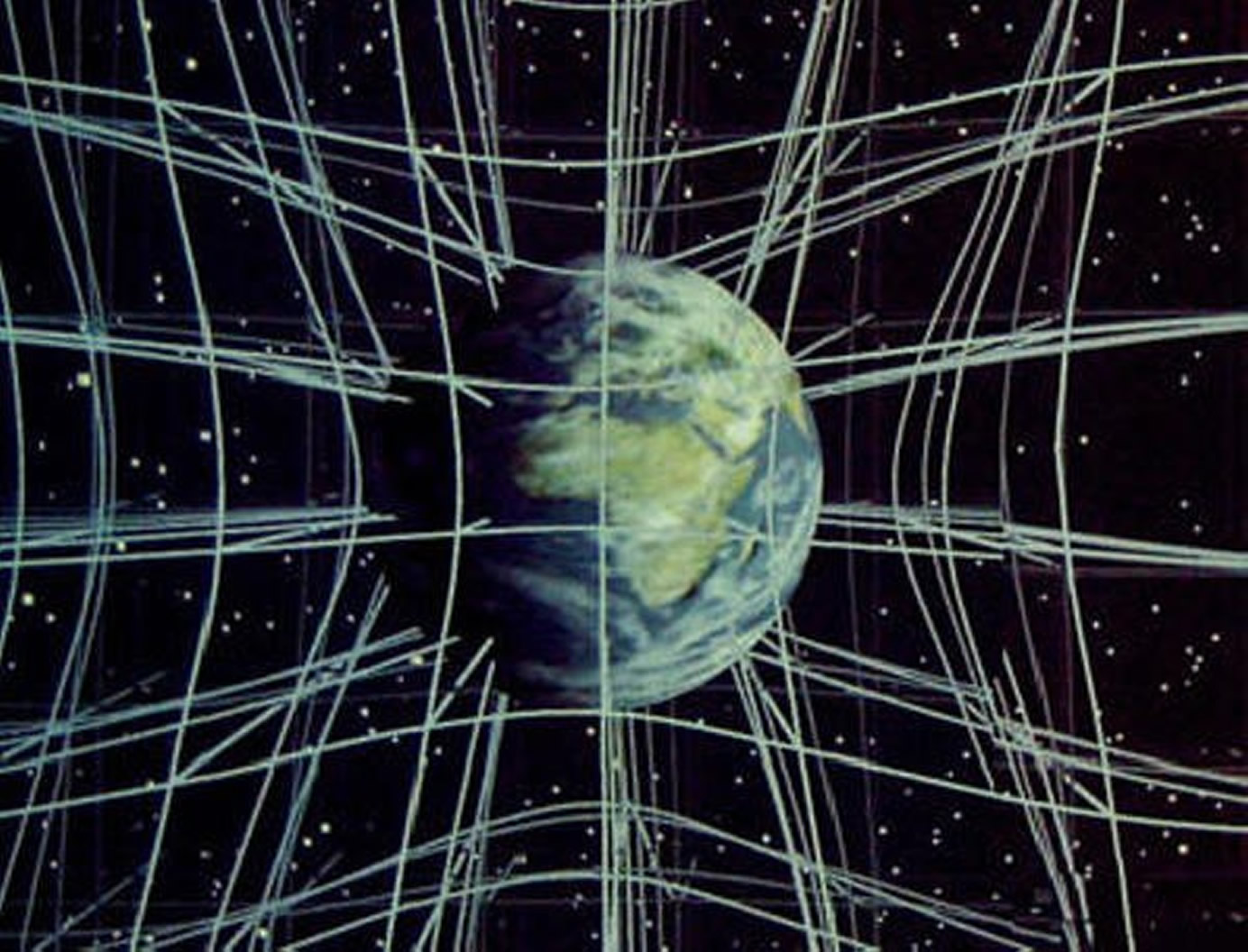
Bild. Die Verzerrung des Raumzeitgewebes.
R: Wie beschreiben wir die Physik und Mechanik als zwei Prinzipien in der Wissenschaft?
A: Ich denke, dass die Physik eine Wirklichkeit beschreibt, die unabhängig von unserer Erkenntnis von ihr ist. Die Aufgabe der Physik besteht darin, die allgemeinsten Naturgesetzte zu finden, anhand derer die vielfältigen Phänomene, die die Natur aufweist, alle erklärt werden können.
Bild. Physik, was in der Schule unterrichtet wird.
Die klassische Physik orientiert sich an Sinneswahrnehmungen, verfeinert durch Messgeräte und mathematischer Gleichungen. Klassische Physik ist mit den Experimenten verbunden. Der Teilchenbeschleuniger Large Hadron Collider am europäischen Kernforschungszentrum CERN bei Genf ist das grösste und aufwendigste technologische Projekt der Menschheit. Über 900 Ingenieure und Wissenschaftler aus 500 Instituten und 80 Ländern sind an der rund vier Milliarden Euro teuren Erkenntnismaschine beteiligt – und das im Gegensatz zu allen anderen Grossprojekten ohne rigide Hierarchien und in einem eigenverantwortlichen Zusammenschluss vieler unabhängiger Forschungseinrichtungen weltweit.
Bild. Die Kollision zwei subatomare Teilchen in einem Teilchenbeschleuniger.
Und die Mechanik ist eine mathematische Beschreibung eines physikalischen Gegenstandes und dessen Bewegung. Die Aufgabe der klassischen Mechanik besteht darin, die Zukunft vorherzusagen. Durch Berechnung wird die Bewegung eines physikalischen Phänomens dargestellt und somit wird ihre Zukunft vorhergesagt.
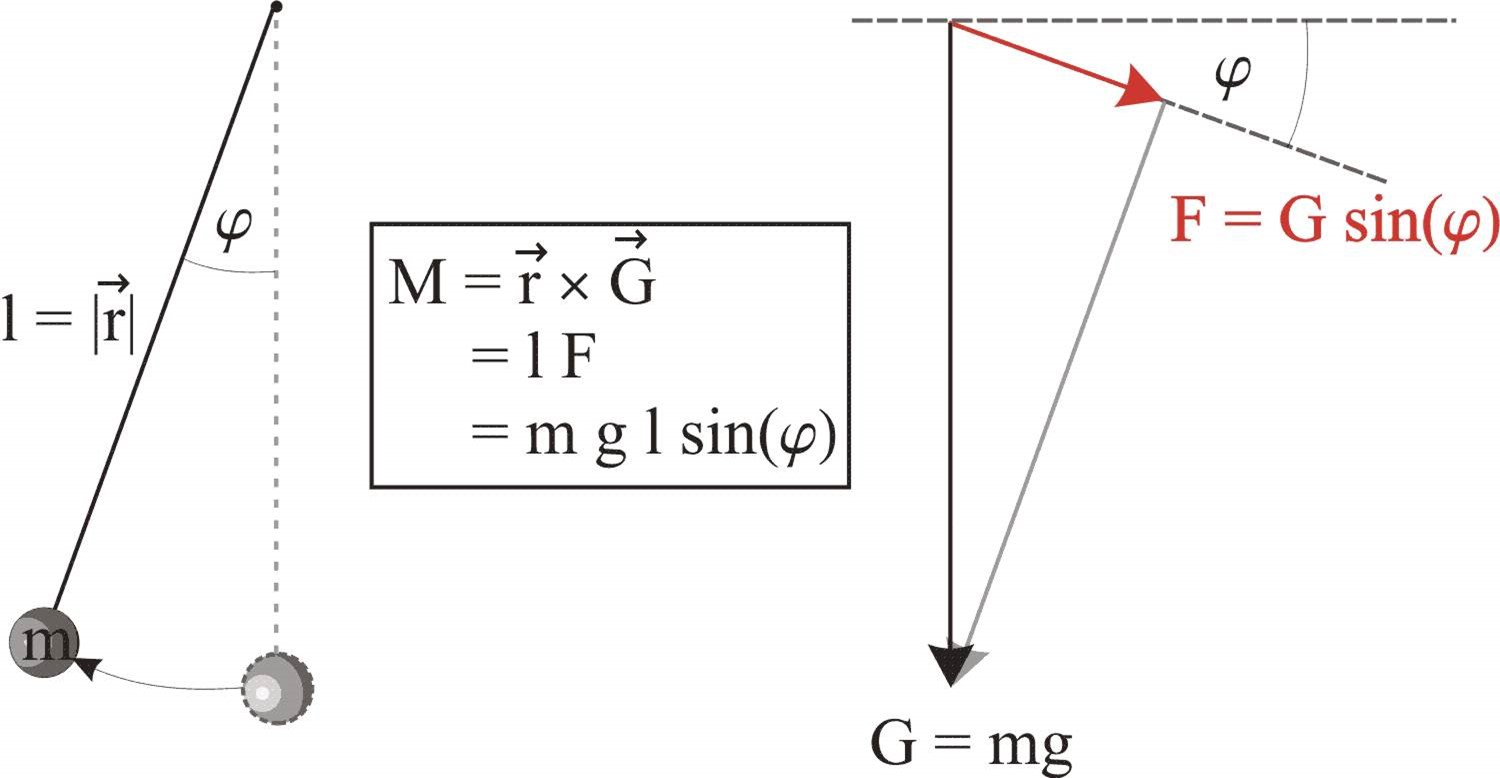
Bild. Mathematische und geometrische Darstellung eines Pendels in der klassischen Mechanik.
R: Erzähle weiter!
A: Eben, die klassische Mechanik beruht auf Gleichungen, die Newton Ende des siebzehnten Jahrhunderts herausgefunden hatte. Der Elektromagnetismus stützt sich auf Gleichungen, die Maxwell Ende des neunzehnten Jahrhunderts aufstellte. Die spezielle Relativitätstheorie fusst auf Gleichungen, die Einstein 1905 entwickelte, und die allgemeine Relativitätstheorie auf Gleichungen, die er 1915 entdeckte. Vieles von dem, was wir physikalisch erfahren, ist mathematisch in Newtons Physik erfasst. Dennoch erweist sich die Wirklichkeit, die sie beschreibt, nicht als die Wirklichkeit unserer Welt. Wir leben in einer relativistischen Wirklichkeit.
R: Möchtest du etwas trinken?
A: Gerne, wenn es dir nichts ausmacht, möchte ich einen Tee!
R: Einen Schwarzen mit zwei Zuckerwürfeln?
A: Ja, danke!
R: Nicht zu danken! Das dauert schon. Erzähle weiter, ich höre dir gerne zu!
A: Laut Einstein verstreicht die Zeit mit unterschiedlichem Tempo, je nachdem, wie schnell wir uns bewegen. Genauer: Je schneller wir uns bewegen, desto langsamer schreitet die Zeit fort. Die Zeit ist nicht absolut, wie einst Newton glaubte.
R: Was glaubte Newton?
A: Er war der Meinung, die Zeit verstreiche überall im Universum gleichförmig, sodass eine Sekunde auf der Erde absolut identisch mit einer Sekunde auf Jupiter oder Mars sei. Die Uhren würden überall im Universum mit gleicher Geschwindigkeit und zwar absolut synchron ticken. Nach Einstein ticken verschiedene Uhren in den Weiten des Universums mit verschieden Geschwindigkeit.
R: Erzähle weiter!
A: Wenn sich die Zeit abhängig von ihrer Geschwindigkeit verändern kann, dann ist, wie Einstein erkannte, auch davon auszugehen, dass sich andere Grössen wie Länge, Masse und Energie verändern. Je schneller man sich bewegt, desto stärker schrumpfen Entfernungen. Entsprechend gilt, je schneller wir uns bewegen, desto mehr nimmt unsere Masse zu. Es bedeutet: Wenn du dich der Lichtgeschwindigkeit nähern würdest, käme die Zeit sogar zum Stillstand; Entfernungen würden auf null schrumpfen und deine Masse wüchse ins Unendliche.
R: Einstein veränderte unsere Vorstellung von der Bühne des Lebens!
A: Bestimmt. In Einstein Universum tragen alle Schauspieler Armbanduhren, die verschiedene Zeiten zeigen. Mit anderen Worten, es ist unmöglich, alle Uhren auf der Bühne synchron anzustimmen. Wenn unter diesen Umständen die Probe auf 12 Uhr mittags festgesetzt wird, bedeutet das für verschiedene Schauspieler Verschiedenes. Tatsächlich ereignen sich merkwürdige Dinge, wenn die Schauspieler aussergewöhnlich rasch über die Bühne eilen. Je schneller sie sich bewegen, desto langsamer ticken ihre Uhren und desto massereicher und schmaler werden ihre Körper. Für Einstein wurde die Bühne selbst ein wichtiger Teil des Lebens. In Einsteins Universum waren Raum und Zeit kein unveränderlicher Schauplatz, sondern ein aktives, dynamisches Element, das sich auf merkwürdige Weise verzerrte und krümmte.
Bild. Die Verzerrung der Zeit auf der Einsteins Bühne.
R: Der Tee ist bereit, ich schenke dir und mir einen frischen Tee ein!
A: Danke für den Tee, er riecht wie immer frisch!
R: Gern Geschehen! Wenn wir mit der Bahn fahren oder mit dem Flugzeug fliegen, erfahren und erleben wir dann Newtons Gleichungen. Newtonschen Physik ist in unserem Alltag verankert. Wir können schnell nach einem herabfallenden Glas greifen, weil wir seine newtonsche Flugbahn intuitiv und augenblicklich erfassen. Newtons Physik erweist sich in vielen Situationen als eine exakte und nützliche Näherung.
Bild. Newtons Physik im Alltag.
A: Richtig. Nützlichkeit und Wirklichkeit sind allerdings höchst unterschiedliche Massstäbe. Der Tee schmeckt gut, wo hast du ihn gekauft?
R: Ich habe diesen Schwarztee im Bioladen gekauft!
A: Nun, es zählt zu den wesentlichen Eigenschaften der klassischen Physik, dass sich, wenn wir die Orte und Geschwindigkeiten aller Objekte zu einem bestimmten Zeitpunkt kennen, mit Hilfe der Newtonschen Gleichungen und ihrer Maxwellschen Aktualisierungen die Aufenthaltsorte und Geschwindigkeiten dieser Objekte auch zu jedem anderen beliebigen Zeitpunkt in der Vergangenheit oder Zukunft bestimmen lassen. Die klassische Physik erklärt unzweideutig, Vergangenheit und Zukunft seien in die Gegenwart eingeätzt. In den Gleichungen findet sich ein einziger Anhaltspunkt, der die «Vorwärtszeit» von der «Rückwärtszeit» unterschiedet. Dies führt uns zur vollständigen Erkenntnis, nämlich, dass die Vergangenheit und die Zukunft vollkommen gleichgestellt sind.
R: Machen wir eine kurze Pause!
A: Das machen wir!
—
—
R: Oh du bist wieder da, ich schenke dir und mir einen frischen Tee ein und setzte mich dir gegenüber an den Kuchentisch hin, und?
A: Der Tee schmeckt gut! Wie heisst dieser Tee?
R: Das ist ein Früchtetee!
A: Wo hast du ihn gekauft?
R: Ich habe ihn in der Bären-Apotheke am Stauffacher gekauft.
A: In der Schule warst du gut in Mathematik!
R: Mathematik ist eine Zaubersprache!
A: Während der Schulzeit hast du immer eine spezielle Zahl gehabt!
R: Ja, eben 6174. Die Zahl 6174 ist vierstellig. Wenn wir diese vierstellige Zahl von 1 bis 7 aufstellen, dann ergibt sich 1467. Und wenn wir 6174 von 7 ausgehen, zurück bis 1, ergibt das die Zahl 7641. Nun, wenn wir von 7641, 1467 abziehen, dann haben wir wieder die Zahl 6174.
A: Eine Magie durch Umstellung!
R: Woran erinnerst du dich, wenn du an Mathematikstunden in der Schule denkst?
A: Viele dieser Stunden waren mit Geometrie, Algebra, Logarithmus verbunden. Ich erinnere mich vor allem an Zahlen!
R: Zahlen werden demnach nicht einfach nur als Mittel gesehen, um die Menge oder Anzahl von irgendetwas zu notieren, vielmehr gilt es, die zu entdecken, und man betrachtet sie als formende Prinzipien, die in der Natur wirken. Alles im Universum – angefangen von materiellen Gegenständen wie der Erde bis zu abstrakten Konzepten wie Gerechtigkeit – ist durch und durch Zahl. Die mächtige Vorstellung, «Zahlen sind alles», die der Mathematik zugrunde liegt folglich entscheidend für ein tieferes Verständnis der Welt ist, wird Pythagoras zugeschrieben. Wahrscheinlich war er der Überzeugung, dass Zahlen und Formen ausserhalb der Welt eine eigene Existenz besässen.
A: Ich erinnere mich an den Satz von Pythagoras und zwar an das Quadrat der Hypotenuse ist gleich der Summe der Quadrate der zwei rechtwinkeligen Seiten.
Bild. Pythagoras Formel.
R: Dem Legende zufolge bemerkte Pythagoras in einer Schmiede, dass Verhältnis der Grössen verschiedener Ambosse mit harmonischen Intervallen verbunden ist. Pythagoras erkannte eine einfache rechnerische Beziehung zwischen den Intervallen wie Oktave, Quinte und Quarte.
A: Möchtest du etwas trinken?
R: Nein, danke!
A: Erzähle weiter!
R: Betrachten wir einmal die Anzahl der Tage in einem Jahr – 365. Wir können leicht nachprüfen, dass 365 die Summe aus drei aufeinanderfolgenden Quadratzahlen ist: 365 = 10² + 11² + 12². Aber das ist noch nicht alles, 365 ist auch die Summe der beiden nächsten Quadratzahlen (365 = 13² + 14²)! Oder betrachten wir die Tage des mittleren Mondmonate: 28. Diese Zahl ist die Summe all ihrer Divisoren oder Teiler (der Zahlen durch die sie ohne Rest teilbar ist): 28 = 1 + 2 + 4 + 7 + 14. Man kann auch beachten, dass 28 die Summe der dritten Potenz der beiden ersten ungeraden Zahlen ist: 28 = 1³ + 3³. Selbst eine Zahl, die in unserem Dezimalsystem so weidlich zur Anwendung gelangt wie die 100, hat ihre eigenen Besonderheiten: 100 = 1³ + 2³ + 3³ + 4³. Was meinst du, soll ich so weiterfahren?
A: Ja!
R: Eben, auch in der Folge der ungeraden ganzen Zahlen 1, 3, 5, 7, 9, … ergibt die Summe aus zwei aufeinanderfolgenden Elementen (von 1 ausgehend) stets eine Quadratzahl. Zum Beispiel:1 = 1², 1 + 3 = 4 = 2², 1 + 3 + 5 = 9 = 3², 1 + 3 + 5 + 7 = 16 = 4², 1 + 3 + 5 + 7 + 9 = 25 = 5² und so weiter.
A: Zahlen üben eine gewisse Faszination aus. Ich habe viel von dem Fibonacci-Zahlen gehört! Würdest du sie bitte schildern?
Bild. Fibonacci Zahlen in der Botanik.
R: Besagte Fibonacci-Zahlen lauten: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 114, 233, … und sind dadurch bestimmt, dass ab dem dritten Glied der Reihe jede Folgezahl die Summe ihrer beiden Vorgänger ist: 1+1 ist 2, 2+1 ist 3, 3+2 ist 5, 5+3 ist 8, 8+5 ist 13, 13+8 ist 21, und so weiter. Wenn wir nun jede Zahl in dieser Reihe durch ihren unmittelbaren Vorgänger teilen (zum Beispiel 144 : 89, 233 : 144, … ) werden wir feststellen, dass die Quotienten in ihrem Wert um den Goldenen Schnitt herumpendeln und sich diesem immer weiter annähern. So erhält man zum Beispiel folgende Ergebnisse (auf die sechste Stelle hinter dem Komma gerundet): Die Zahl, 144: 89 = 1,617978, Die Zahl 233 : 144 = 1, 618056, Die Zahl 377 : 233 = 1, 618026 und so weiter. Fibonacci Zahlen erscheinen in der Natur sehr häufig und lassen sich in der Anzahl von Blütenblättern ablesen vor allem bei Gänseblümchen. Wenn man zum Beispiel die Unterseite eines Tannenzapfens ansieht, erkennt man spiralförmige Linien zwischen den Samenschuppen, und wenn man diese Spiralen zählt, erhält man in der Regel eine Fibonacci Zahlen, zählt man sie in entgegengesetzter Richtung, erhält man eine benachbarte Fibonacci Zahlen.
Bild. Fibonacci Zahlen beim Tannenzapfen.
Dies trifft auch auf die Samen in den Köpfen der Sonnenblume zu, nämlich zwei Spiralsätze und wenn man die Spiralen beide Richtungen zählt, erhält man jeweils Fibonacci Zahlen.
Bild. Fibonacci Zahlen bei Sonnenblume.
A: Unsere Mathematik ist eine Kombination aus Erfindungen und Entdeckungen!
R: In der Tat ist die Mathematik eine Richtschnur. In Jahrhunderten naturwissenschaftlicher Forschung hat sich die Mathematik als eine leistungsfähige und prägnante Sprache zur Analyse des Universums erwiesen. Tatsächlich gibt es in der modernen Wissenschaftsgeschichte eine Fülle von Beispielen, in denen die mathematische Beschreibung zu Voraussagen führte.
A: Würdest du sie bitte veranschaulichen?
R: Gerne. Zum Beispiel, dass es im Universum Schwarze Löcher gibt, dass das Universum Antimaterie enthält, dass weit voneinander entfernte Teilchen verschränket sein können. All diese wurden durch Experimente und Beobachtungen bestätigt. Diese Erfindungen haben die Grundeinstellung in der theoretischen Physik nachhaltig beeinflusst. Heutzutage sind einige Wissenschaftler der Meinung, dass die Mathematik ein bewährter Weg zur Wahrheit ist.
A: Es sieht so aus, dass die Mathematische Objekte wie Würfel oder natürliche Zahlen ihre Gegenstücke in der realen Welt haben!
R: Wir existieren in drei verschieden «Welten»: in der Welt unserer Wahrnehmung, in der physikalischen Welt und in einer plantonischen Welt der mathematischen Formen.
Bild. Die plantonische Welt.
Die erste Welt ist die Heimat all unserer mentalen Bilder – wie wir die Gesichter unserer Kinder wahrnehmen, einen atemberaubenden Sonnenuntergang empfinden oder auf die entsetzlichen Bilder eines Krieges reagieren. Dies ist auch die Welt, in der Liebe, Eifersucht und Vorurteile ihren Sitz haben, ebenso unsere Wahrnehmung von Musik, des Geruchs von Essen und von Angst. Die zweite Welt ist jene, die wir normalerweise als physikalische Realität betrachten. Real vorhandene Blumen, Aspirin-Tabletten, weisse Wolken und Düsenflugzeuge haben ihren Platz in dieser Welt, dazu Galaxien, Planeten, Atome, Pavianherzen und menschliche Gehirne. Und die dritte Welt nämlich die platonische Welt der mathematischen Formen, die eine eigene, der physikalischen und mentalen Welt vergleichbare Realität besitzt, ist das Mutterland der Mathematik. Sie ist der Ort, an dem wir die natürlichen Zahlen 1, 2, 3, 4, … antreffen, dazu all die Formen und Lehrsätze der Geometrie, Newtons Bewegungsgesetze, Einsteins Gleichungen, String- und Katastrophentheorie sowie mathematische Modelle zur Beschreibung des Aktienmarktverhaltens.
A: Bemerkenswert, erzähle weiter!
R: Die physikalische Welt scheint Gesetzen zu gehorchen, die eigentlich in der Welt der mathematischen Formen beheimatet sind und unser wahrnehmendes Bewusstsein ist imstande, Zugang zur mathematischen Welt zu erlangen, indem es einen Schatz an abstrakten mathematischen Formen und Konzepten entdeckt oder schafft und formuliert.
A: Beeindruckend, erzähle weiter!
R: Einige der Philosophen des antiken Griechenlands – allen voran Pythagoras und Platon – waren bereits voller Ehrfurcht für die der Mathematik augenscheinlich innewohnende Fähigkeit, das Universum nach ihren Regeln zu formen und zu lenken, obwohl sie offenbar jenseits aller menschlichen Macht, sie zu ändern, zu bestimmen oder zu beeinflussen, existiert. Sogar fragte sich Einstein: «Wie ist es möglich, dass die Mathematik, die noch von aller Erfahrung unabhängiges Produkt des menschlichen Denkens ist, auf die Gegenstände der Welt so vortrefflich passt?» Einige Wissenschaftler sind der Auffassung, dass alle Naturereignisse von mathematischen Gesetzen gelenkt und alle Strukturen, natürlich wie von Menschenhand geschaffene, von geometrischen Proportionen bestimmt werden.
A: Interessant, was manche Forscher meinen. Gemäss deren Überzeugungen kann behauptet werden, dass die Mathematik die Grundlage allen Seins und die Geometrie die höchste Form der Mathematik ist!
F: Der Physiker Max Tegmark von MIT (Massachusetts Institute of Technology) sieht Ähnlichkeiten zwischen unserer Welt und der Welt eines Computerspiels. In einem Interview bemerkte er: «Wenn ich eine Figur in einem Computerspiel wäre, das technisch so entwickelt wäre, dass ich ein Bewusstsein hätte und diese Welt dort forschen könnte, dann hätte ich das Empfinden, sie bestehe aus realen festen Objekten. Aber wenn ich als neugieriger Physiker anfangen würde, die Eigenschaften dieser Dinge zu erforschen, die Gleichungen durch die sich die Dinge bewegen und die den Dingen ihre Eigenschaften verleihen, dann würde ich feststellen, dass das Alles mathematische Eigenschaften sind, die nämlich der Programmierer in die Software, die alles beschreibt, einprogrammiert hat. Die physikalischen Gesetze in einem Spiel zum Beispiel, wie ein Objekt schwebt, hüpft oder abstürzt sind nur mathematische Regeln, erschaffen von einem Programmierer. Letztlich besteht das ganze Universum wie eines Computerspieles nur aus Zahlen und Gleichungen. Und genau das widerfährt mir auch in dieser Realität. Dinge zum Beispiel meine Arme, die nicht mathematisch erscheinen, stellen sich bei genauer Betrachtung als umso mathematischer heraus».
Bild. Mehrere mathematische Formeln schweben über zwei Hände.
A: Ist unsere Welt also genauso mathematisch wie eine Computerspielrealität?
R: In der Tat unterscheidet sich die Software Welt eines Spiels nicht so sehr von der physikalischen Welt, in der wir leben. Die Mathematik beschreibt die Realität plausibel. Es herrscht eine enge Verbindung zwischen der physischen Welt und der Welt der Mathematik. Wenn du das Foto, das an der Wand hängt, anschaust, was siehst du dann?
A: Ich sehe den Zürichsee.
R: Der Physiker Max Tegmark ist der Meinung, wenn wir das Bild aus nächster Nähe betrachten, können wir dann sehen, dass es eigentlich ein Pixelfeld ist, wobei für jedes Pixel drei Zahlen die Werte von Rot, Grün und Blau definieren.
Bild. Farben, die ein Auge aufnimmt.
A: Ich kann dir nicht folgen!
R: Das Licht, das wir wahrnehmen, besteht aus Zahlen. Das sichtbare Lichts Spektrum variiert von 400 Nanometer bis 700 Nanometer, von der Farbe Blau bis zur Farbe Rot.
Bild. Das Lichts Spektrum, das wir empfinden.
A: Was ist ein Nanometer?
R: Der Nanometer ist eine Längeneinheit im metrischen System, die einem Milliardstel Meter entspricht.
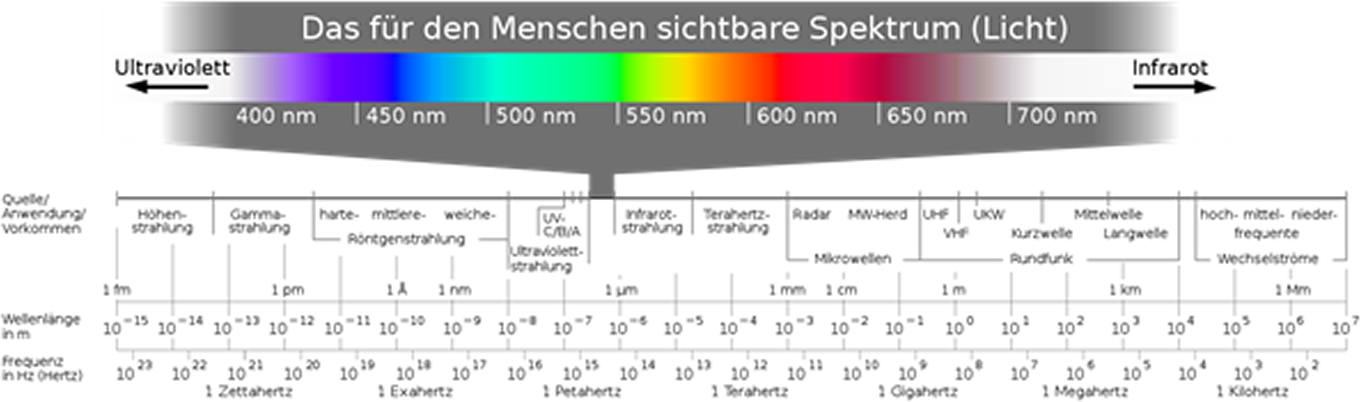Bild. Die Gesamtheit aller elektromagnetischen Wellen
A: Fassen wir zusammen?
R: Das machen wir!
A: Die Macht der Physik stammt von ihren Gesetzen, die diktieren, wie sich die Natur in der Zeit verändert. Sie tun dies, indem sie den Zustand der Welt zum jetzigen Zeitpunkt in den Zustand zu jedem beliebigen zukünftigen Zeitpunkt verwandeln. Ein Gesetz der Physik verhält sich in gewissen Hinsichten wie ein Computerprogramm: Es liest Inputs ein und gibt einen Output aus. Der Input ist der Zustand zu einem bestimmten Zeitpunkt; der Output ist der Zustand zu einem zukünftigen Zeitpunkt. Die Physik ist die Weise, in der ein Atom die Atome kennt.
R: Mathematik ist ein natürlicher Bestanteil unseres Menschseins. Sie entspringt unserem Körper, unserem Gehirn und unseren Alltagserfahrungen in der Welt. Mathematik ist ein Teil der Physikalischen Welt. Das Herz der Mathematik sind Zahlen. Null ist eine Zahl. Der Nachfolger einer jeden Zahl ist ebenfalls eine Zahl. Es gibt keine zwei Zahlen, die denselben Nachfolger haben. Zahlen ermöglichen uns die Zeit zu strukturieren und vergesse nicht, die Zeit ist eine mathematische Konstruktion.
Quellen:
Askew, Mike & Ebbutt, Scheila. Geometrie. Niederland: Librero, 2016.
Greene, Brian. Der Stoff, aus dem der Kosmos ist. München: Wilhelm Goldmann, 2008.
Greene, Brian. Bis zum Ende der Zeit. München: Siedler, 2020.
Hart-Davis, Adam. Schrödingers Katze. München: Knesebeck, 2019.
Kaku, Michio. Im Paralleluniversum. Reinbek bei Hamburg: Rowohlt, 2014.
Kaku, Michio. Die Physik der unsichtbaren Dimensionen. Reinbek bei Hamburg: Rowohlt, 2015.
Livio, Mario. Ist Gott ein Mathematiker. München: C.H. Beck, 2017
Randall, Lisa. Verborgene Universen. Frankfurt am Main: Fischer, 2013
Smolin, Lee. Quantenwelt. München: Anstalt, 2019.
Susskind, Leonard & Hrabovsky, George E. Klassische Mechanik: Das Theoretische Minimum. Berlin: Springer, 2020.
Vaas, Rüdiger. Vom Gottesteilchen zur Weltformel. Stuttgart: Franckh-kosmos, 2013.
Wade, David. Geometrie und Kunst. Niederlande: Librero, 2017